
First, we need to factorize the quadratic expressions. To do this we need to find the roots of each quadratic expression. In the function of the numerator, the coefficients are: a = 1, b = -4, and c = 3. Applying the quadratic formula, the roots are:
![\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{4\pm\sqrt[]{(-4)^2-4\cdot1\cdot3}}{2\cdot1} \\ x_(1,2)=\frac{4\pm\sqrt[]{4}}{2} \\ x_1=(4+2)/(2)=3 \\ x_2=(4-2)/(2)=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5fci4u33iwnrt6m21b8ihru9sy8obv4qim.png)
Then, we can express the function with its roots as follows:

In the first function of the denominator, the coefficients are: a = 1, b = 1, and c = -2. Applying the quadratic formula, the roots are:
![\begin{gathered} x_(1,2)=\frac{-1\pm\sqrt[]{1^2-4\cdot1\cdot(-2)}}{2\cdot1} \\ x_(1,2)=\frac{-1\pm\sqrt[]{9}}{2} \\ x_1=(-1+3)/(2)=1 \\ x_2=(-1-3)/(2)=-2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bhjkn81bubyvdaoqa7ppn5lxd0n1qwxpvd.png)
Then, we can express the function with its roots as follows:
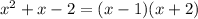
In the second function of the denominator, the coefficients are: a = 1, b = -2, and c = -3. Applying the quadratic formula, the roots are:
![\begin{gathered} x_(1,2)=\frac{2\pm\sqrt[]{(-2)^2-4\cdot1\cdot(-3)}}{2\cdot1} \\ x_(1,2)=\frac{2\pm\sqrt[]{16}}{2} \\ x_1=(2+4)/(2)=3 \\ x_2=(2-4)/(2)=-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ohpw3ltrycve33pj3euiwute98rizn2z8z.png)
Then, we can express the function with its roots as follows:
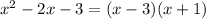
Substituting the equivalent expression into the original rational function, we get:
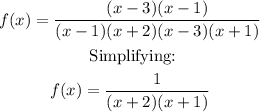
After the simplification, the discontinuities at x = 3 and x = 1 have been removed. x = 1 belongs to the interval [0.5, 1.5]