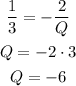Since the solution of the system is any point (x, y) where the relation between x and y is given by the equation x - 3y = 4, that means the system has an infinite number of solutions, therefore the second equation of the system is a line paralell to the line of the first equation.
Calculating the slope of each equation, we have:
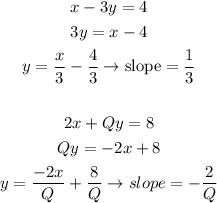
Since the lines are paralell, they have the same slope, so: