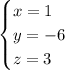Question

2x-y-3z=1 / 4x+3y+2z=-4 / -3x+2y+5z=-3 solve using elimination

Answer 1

x = 2

y = -6

z = 3

`\begin{cases}E_1\Rightarrow2x-y-3z=1 \\ E_2\Rightarrow4x+3y+2z=-4 \\ E_3\Rightarrow-3x+2y+5z=-3\end{cases}`

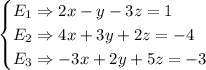
I named the equation to make it more simple.

To solve for elimination, we can multiply E1 by (-2) to eliminate the 4x in E2

`\begin{gathered} (4x+3y+2z=-4)+(-2)(2x-y-3z=1)\Rightarrow0x+5y+8z=-6 \\ \end{gathered}`

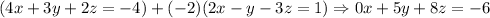
Now the system is:

`\begin{cases}E_1\Rightarrow2x-y-3z=1 \\ E_2\Rightarrow5y+8z=-6 \\ E_3\Rightarrow-3x+2y+5z=-3\end{cases}`

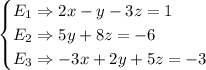
We can continue by eliminating the (-3x) in E3. THen multiply E1 by (3/2) and add it to E3:

`(-3x+2y+5z=-3)+(3)/(2)(2x-y-3z=1)\Rightarrow0x+(1)/(2)y+(1)/(2)z=-(3)/(2)`

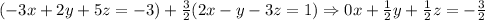
Now the system is:

`\begin{cases}E_1\Rightarrow2x-y-3z=1 \\ E_2\Rightarrow5y+8z=-6 \\ E_3\Rightarrow(1)/(2)y+(1)/(2)z=-(3)/(2)\end{cases}`

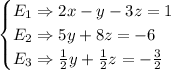
Let's continue by eliminating y. Then we multiply E2 by -(1/10) and add it to E3:

`((1)/(2)y+(1)/(2)z=-(3)/(2))+(-(1)/(10))(5y+8z=-6)\Rightarrow0y-(3)/(10)z=-(9)/(10)`

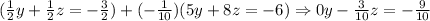
The system is now:

`\begin{cases}E_1\Rightarrow2x-y-3z=1 \\ E_2\Rightarrow5y+8z=-6 \\ E_3\Rightarrow-(3)/(10)z=-(9)/(10)\end{cases}`

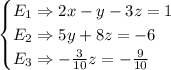
Now we can know the value of z:

`-(3)/(10)z=-(9)/(10)\Rightarrow z=(-(9)/(10))\cdot(-(10)/(3))=3`
`\begin{cases}E_1\Rightarrow2x-y-3z=1 \\ E_2\Rightarrow5y+8z=-6 \\ E_3\Rightarrow z=3\end{cases}`

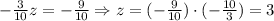
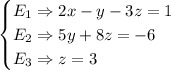
Now we can replace z in E2:

`\begin{gathered} 5y+8\cdot3=-6 \\ y=-(30)/(5) \\ y=-6 \end{gathered}`
`\begin{cases}E_1\Rightarrow2x-y-3z=1 \\ E_2\Rightarrow y=-6 \\ E_3\Rightarrow z=3\end{cases}`

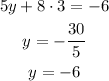
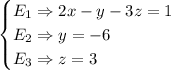
Finally, replace y and z in E1:

`\begin{gathered} 2x-y-3z=1\Rightarrow2x-(-6)-3\cdot3=1 \\ x=(4)/(2)=2 \end{gathered}`

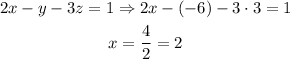
The solution of the equation is:

`\begin{cases}x=1 \\ y=-6 \\ z=3\end{cases}`