1 Answer

Ask a Question

Daniel Porteous · Answer 1 · 2023-11-05T12:55:06+0000

Probability:

Women (W)= 130

Men (M) = 400 - 130 = 270

Total = 400

Prob(W) = 130/400 = 13/40

Prob(M) = 270/400 = 27/40

a. Probability of selecting one woman out of 3 applicants:

Possible outcomes = {WMM, MWM, or MMW}

$\begin{gathered} \text{Prob(One Woman)}=\text{ (}(13)/(40)*(27)/(39)*(26)/(38))\text{ +(}(27)/(40)*(13)/(39)*(26)/(38))\text{ + (}(27)/(40)*(26)/(39)*(13)/(38))\text{ = 3 x( }(27)/(40)*(26)/(39)*(13)/(38)) \\ \\ \text{ = 0.4618 }\approx\text{ 0.46} \end{gathered}$

b. Possible outcomes = {WWM, WMW, or MWW}

$\begin{gathered} \text{Prob(Two Women) = (}(13)/(40)*(12)/(39)*(27)/(38))\text{ + (}(13)/(40)*(27)/(39)*(12)/(38))\text{ + (}(27)/(40)*(13)/(39)*(12)/(38))\text{ = 3(}(13)/(40)*(12)/(39)*(27)/(38)) \\ \\ \text{ = 0.213 }\approx\text{ 0.21} \end{gathered}$

c. Possible outcomes = (WWW)

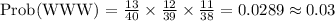
$\text{Prob(WWW) = }(13)/(40)*(12)/(39)*(11)/(38)=0.0289\approx0.03$

d.

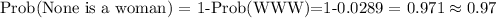
$\text{Prob(None is a woman) = 1-Prob(WWW)=1-0.0289 = 0.971}\approx0.97$

The correct answers are: a. 0.46

b. 0.21

c. 0.03

d. 0.97

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions