Question

Find the Mean, Median, Mode and Range 63,25,43,28,72,61,45,46,13

Answer 1

Given

The data, 63,25,43,28,72,61,45,46,13.

To find the mean, median, mode and range.

Step-by-step explanation:

It is given that,

63,25,43,28,72,61,45,46,13.

Arrange the given data in ascending order.

That implies,

13,25,28,43,45,46,61,63,72.

Then, the mean of the given data is,

`\begin{gathered} mean=(13+25+28+43+45+46+61+63+72)/(9) \\ =(396)/(9) \\ =44 \end{gathered}`

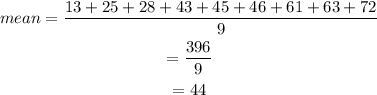
Also, the median of the given data is,

`\begin{gathered} median=((n+1)/(2))th\text{ }term[\because n\text{ }is\text{ }odd] \\ =((9+1)/(2))th\text{ }term \\ =((10)/(2))th\text{ }term \\ =5th\text{ }term \\ =45 \end{gathered}`

Also, the mode of the given data is,

In the given data, no observation occurs more than once.

That implies,

`mode=0`

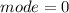
Also, the range of the given data is,

`\begin{gathered} Range=Higher\text{ }value-Lower\text{ }value \\ =72-13 \\ =59 \end{gathered}`

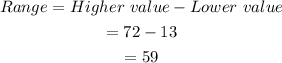
Hence, the mean is 44, the median is 45, the mode is 0, and the range is 59.