Question

You want to buy a $34,000 car. The company is offering a 2% interest rate for 60 months (5 years). What willyour monthly payments be?

Answer 1

We have to calculate the monthly payments for an annuity of $34,000 with a 2% interest rate for 60 months.

We then can express the monthly payment as:

`\text{PMT}=(PV\cdot(r)/(m))/(1-(1+(r)/(m))^(-n\cdot m))`

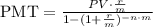
where PV = 34000, r = 0.02 (the annual interest rate in decimal form), m = 12 (number of subperiods per year) and n = 5 (the number of annual periods).

We can replace with the values and solve for PMT as:

`\begin{gathered} \text{PMT}=(34000\cdot(0.02)/(12))/(1-(1+(0.02)/(12))^(-5\cdot12)) \\ \text{PMT}\approx(34000\cdot0.00167)/(1-(1.00167)^(-60)) \\ \text{PMT}\approx(56.67)/(1-0.905) \\ \text{PMT}\approx(56.67)/(0.095) \\ \text{PMT}\approx595.94 \end{gathered}`

Answer: the monthly payments will be approximately $595.94.