Givens.
• The height of the tower is h = 9.0 m.
,
• The bulls-eye is 3.5 m away from the tower, x = 3.5 m.
Before we find the needed speed to hit the bulls-eye, we need to find the time. Use a formula that includes height, gravity, and time.
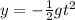
This formula does not show the initial velocity because is null. Use the given magnitudes and solve for t.
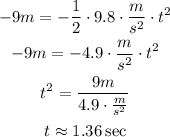
Find the final velocity. In this case, use the formula for a constant motion because the pumpkin is thrown horizontally, and the horizontal motion is constant.
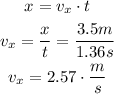
Therefore, the needed speed to hit the bulls-eye is 2.57 m/s.