Question

Given:• PQRS is a rectangle.• mZ1 = 50°Р21SRWhat is mZ2?130°85°70°65°

Answer 1

To answer this question, we need to recall that: "the diagonals of a rectangle bisect each other"

Thus, if we assign the point of intersection of the two diagonals in the rectangle as point O, we can say that the triangle OQR is an "isosceles triangle". Note that this is because the lengths OR and OQ are equal since we know that: "the diagonals of a rectangle bisect each other". See the below diagram for clarity.

Now, we have to recall that:

- the base angles of any isosceles triangle are equal. This is a fact, and this means that the angles

- also the sum of all the angles in any triangle is 180 degrees

Now, considering the isosceles triangle OQR, we have that:

`\angle OQR+\angle ORQ+\angle ROQ=180^o`

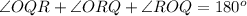
Now, since the figure already shows that angle
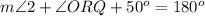`m\angle2+\angle ORQ+50^o=180^o`Now, since we have established that the base angles
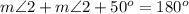`m\angle2+m\angle2+50^o=180^o`we can now solve the above equation for m<2 as follows:

`\begin{gathered} m\angle2+m\angle2+50^o=180^o \\ \Rightarrow2m\angle2+50^o=180^o \\ \Rightarrow2m\angle2=180^o-50^o \\ \Rightarrow2m\angle2=130^o \\ \Rightarrow m\angle2=(130^o)/(2)=65^o \end{gathered}`

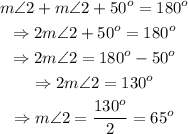
Therefore, the correct answer is: option D