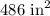We have the given parameters
The dimensions of the small rectangle are
To get the dimension of the big rectangle, we will use the scale factor:

From the image given

To get the dimensions of the big rectangle, we will simply multiply the sides of the small rectangle by the scale factor, so that we will obtain
Since we have gotten the dimensions of the big rectangle, we can now compute the area
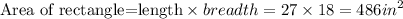
Thus, the answer is option D