If we join the point O and point C by a line then right triangle OBC is formed.
Determine the length of side OC.
![\begin{gathered} (OC)^2=(OB)^2+(BC)^2 \\ =(7)^2+(6)^2 \\ OC=\sqrt[]{85} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r0m2gpnpcgfeobnx282einx8e1cd1twuql.png)
OC is radius of circle with center O. So OC = OD, as both are radius of circle.
Determine the neasure of side DE by using pythagoras theorem in triangle ODE.
![\begin{gathered} (DE)^2=(OD)^2-(OE)^2 \\ =(\sqrt[]{85})^2-(7)^2 \\ =85-49 \\ DE=\sqrt[]{36} \\ =6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/stgj28dmdl2vjnte9022gjwe32segs7jni.png)
Since DE is equal to DF. So DF= 2DE.
Determine the measure of chord DF.
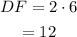
Answer: 12