Answer:
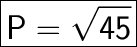
Explanation:
Since, the triangle is a right angled triangle, we can use Pythagoras theorem to find the perpendicular of the triangle.
Which is:
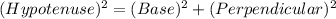
Rearranging
(Perpendicular)² = (Hypotenuse)² - (Base)²
Where P = ?, H = 7 and B = 2
(P)² = (7)² - (2)²
(P)² = 49 - 4
(P)² = 45
Take sqrt on both sides
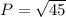
![\rule[225]{225}{2}](https://img.qammunity.org/2023/formulas/english/college/eq413d752mwtrwwenrzwldxt4w1olmf1b3.png)
Hope this helped!
~AH1807