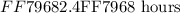Question

How long will your trip take (in hours) if you travel 60 km at an average speed of 25 km/h?

Answer 1

We will investigate the distance - speed - time relationship. The following quantities are defined as followed:

`\text{Distance = d ( km ) , Speed = s ( }(km)/(hr)\text{ ) , Time = t ( hr )}`

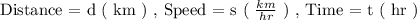
The quantities given are as follows:

`d\text{ = 60 km , s = 25 }(km)/(h)`

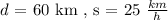
The distance - speed - time relationship is expressed as:

`s\text{ = }(d)/(t)`

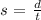
We will use the above relationhsip and determine the amount of time taken to cover 60 km at 25km/h speed:

`\begin{gathered} t\text{ = }(d)/(s) \\ t\text{ = }\frac{60\text{ km}}{25\text{ }(km)/(h)} \\ \textcolor{#FF7968}{t}\text{\textcolor{#FF7968}{ = 2.4 hours}} \end{gathered}`

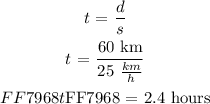
The time it takes to travel the required distance at the rated speed is:

`\textcolor{#FF7968}{2.4}\text{\textcolor{#FF7968}{ hours}}`