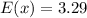Question

Find the expected value for this probability distribution table(will send image)

Answer 1

Given the Distribution Table that shows the Probability Distribution for the number of classes students take, you need to use the following formula for finding the Expected Value:

`E(x)=\sum_^x\cdot p(x)`

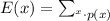
Where "x" is an outcome and this is the probability of the outcome:

`p(x)`

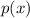
Therefore, using the values provided in the table, you can set up:

`E(x)=(0)(0)+(1)(0.30)+(2)(0.21)+(3)(0.10)+(4)(0.11)+(5)(0.06)+(6)(0.04)+(7)(0.15)+(8)(0.03)`

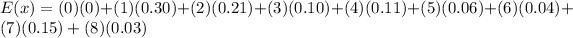
By solving the Multiplications and the Additions, you get:

`E(x)=3.29`

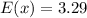
Hence, the answer is:

`E(x)=3.29`