SOLUTION
The triangle is a right angle triangle with the following parameters given in the diagram

Using the trigonometry ratio for the sine of an angle, we have
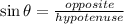
Then we substituting the parameters into the formula above, we obtain
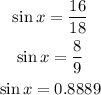
Then the value of x becomes
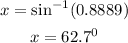
Therefore x= 62.7°