Speed of Car 1: C1
Speed of Car 2: C2
Distance between Car 1 and Car 2: 120 mi
Time to meet: 2 hours
distance is equal to speed multiplied by time

Car 1 travels 6mph faster than Car 2:
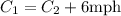
Use the next system of equations:
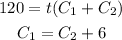
To solve:
1. Substitute the value of C1 in the first equation ofr the given in the second: t=2

2. Solve for C2:
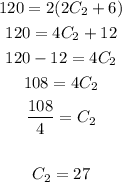
3. Use the value of C2 to find C1:
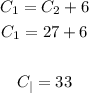
Then, the average spped of car 1 is 33mph and average spped of car 2 is 27mph