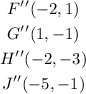Question

Hello, I have tried this practice problem so many times and watched so many math videos and still I am only getting .13 correct. See question attached. Thank you

Answer 1

To solve this problem the first thing we have to do is to find the coordinates of the original points:

`\begin{gathered} F(1,-2) \\ G(3,1) \\ H(5,-2) \\ J(3,-5) \end{gathered}`

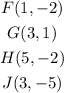
Now that we have the original points we have to remember that a rotation of 90 degrees clockwise is given by:

`(x,y)\rightarrow(y,-x)`

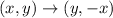
This means that we have to interchange the coordinates and then change the sign of the second one. With this in mind we have:

`\begin{gathered} F^(\prime)(-2,-1) \\ G^(\prime)(1,-3) \\ H^(\prime)(-2,-5) \\ J^(\prime)(-5,-3) \end{gathered}`

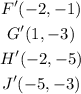
Now we need to translate the coordinates two units up, to do this we have to remember that a general translation is given by:

`(x,y)\rightarrow(x+a,y+b)`

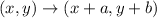
In this case we are only shifting in the y direction, then a=0; furthermore we know that we have to shift the figure two units up this means that b=2. Then in this case we have the translation:

`(x,y)\rightarrow(x,y+2)`

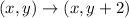
Therefore our final coordinates are:

`\begin{gathered} F^(\prime)^(\prime)(-2,1) \\ G^(\prime)^(\prime)(1,-1) \\ H^(\prime)^(\prime)(-2,-3) \\ J^(\prime)^(\prime)(-5,-1) \end{gathered}`