Question

Finda) The sum of the first 10 termsb) the first term and the common difference

Answer 1

EXPLANATION

As the sum is given by the arithmetic sequence:

`S_n=(3n(n-33))/(2)`

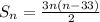
a)

Applying the sumatory to the first 10 terms:

`S_(10)=(3\cdot10(10-33))/(2)`

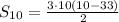
Subtracting numbers:

`S_(10)=(3\cdot10\cdot(-23))/(2)`

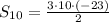
Multiplying numbers:

`S_(10)=(-690)/(2)`

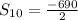
Simplifying:

`-345`

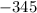
b) The first term is given as shown as follows:

`S_1=(3\cdot1\cdot(1-33))/(2)=(-96)/(2)=-48`

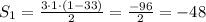
We can get the common difference by computing each subsequent number of the sequence and subtracting to the last one as shown as follows:

`a_2=S_2-(-48)=(3\cdot2\cdot(2-33))/(2)-(-48)=-93+48=-45`

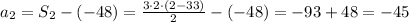
Now, subtracting -45 to the first term -48 give us:

-45 - (-48) = -45 + 48 = -3

In conclusion, the common difference is -3