Question

What is the equation of the line graphed below?A y+1=-3(x-1)B y+1=-3(x-2)C y+2=-3(x-2)D y+2=-3(x-1)

Answer 1

Given the line graphed, you can identify that it passes through this point:

`(0,2)`

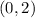
The Point-Slope Form of the equation of a line is:

`y-y_1=m(x-y_1)`

Where "m" is the slope of the line and this is a point on the line:

`(x_1,y_1)`

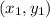
The Slope-Intercept Form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

You can find the slope of the line using this formula:

`m=(y_2-y_1)/(x_2-x_1)`

Where these two points are on the line:

`(x_1,y_1),(x_2,y_2)`

In this case, all the answer choices show that the slope is:

`m=-3`

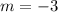
Then, you can substitute a point on the line graph into the equations provided in the answer choices and evaluate, until you find a true equation:

Using the equation given in Option A, you can substitute:

`\begin{gathered} x=0 \\ y=2 \end{gathered}`

You get:

`y+1=-3(x-1)`
`2+1=-3(0-1)`
`3=-3(-1)`
`3=3\text{ \lparen True\rparen}`

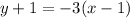
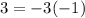
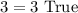
Hence, the answer is: Option A.