Question

im thinking of 2 numbers. The sum of my number is 55. The product of my numbers is 684. What are the 2 numbers? Explain.

Answer 1

Let x and y be the two number. Then, we can write

`\begin{gathered} x+y=55 \\ x\cdot y=684 \end{gathered}`

From the first equation, we have

`y=55-x`

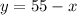
By substituting this result into the second equation, we obtain

`x\mathrm{}(55-x)=684`

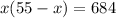
which gives

`55x-x^2=684`

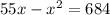
we can rewrite this quadratic equation as follows

`x^2-55x+684=0`

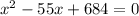
Then, we can apply the quadratic formula, that is,

`x=\frac{-(-55)\pm\sqrt[]{(-55)^2-4(1)(684)}}{2}`

which gives

`\begin{gathered} x=\frac{55+\sqrt[]{3025-2736}}{2} \\ x=(55\pm17)/(2) \end{gathered}`

Then, the 2 solutions for x are

`\begin{gathered} x=(72)/(2)=36 \\ x=(38)/(2)=19 \end{gathered}`

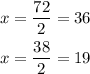
Now, we can substitute these solutions into the equation x.y=684. For the first solution, we have

`\begin{gathered} 36\cdot y=684\Rightarrow y=(684)/(36)=19 \\ \end{gathered}`

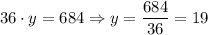
and for the second solution, we have

`19\cdot y=684\Rightarrow y=(684)/(19)=36`

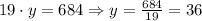
Therefore, the two numbers are 19 and 36