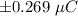Question

Two equally charged, 2.307 g spheres are placed with 3.606 cm between their centers. When released, each begins to accelerate at 216.783 m/s2. What is the magnitude of the charge on each sphere? Express your answer in microCoulombs.

Answer 1

Given:

The equal charges are placed at a distance of

`\begin{gathered} r=3.606\text{ cm} \\ =3.606*10^(-2)\text{ m} \end{gathered}`

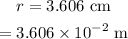
The mass of each charge is,

`\begin{gathered} m=2.307\text{ g} \\ =2.307*10^(-3)\text{ kg} \end{gathered}`

The acceleration of each charge is,

`a=216.783\text{ m/s}^2`

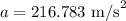
To find:

The magnitude of the charge on each sphere

Step-by-step explanation:

The electric force due to the charges supplies the acceleration of the charges. The electric force is,

`\begin{gathered} F=(kq^2)/(r^2) \\ F=(9*10^9* q^2)/((3.606*10^(-2))^2) \end{gathered}`

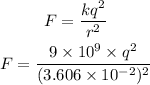
Here, k is the Coulomb constant.

We can write,

`\begin{gathered} F=ma \\ (9*10^9* q^2)/((3.606*10^(-2))^2)=2.307*10^(-3)*216.783 \\ q^2=(2.307*10^(-3)*216.783*(3.606*10^(-2))^2)/(9*10^9) \\ q^2=7.23*10^(-14) \\ q=\pm2.69*10^(-7)\text{ C} \\ q=\pm0.269\text{ }\mu C \end{gathered}`

Hence, the magnitude of each sphere is,

`\pm0.269\text{ }\mu C`