Question

Find the critical value Za/2 that corresponds to the given confidence level.99%

Answer 1

Given the confidence level:

99%

Let's find the critical value that corresponds to the given confidence level.

To find the critical vale, apply the formula:

`(Z_(\alpha))/(2)`

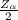
Where α is the level of significance.

To find α, we have:

α = 1 - C

α = 1 - 99% = 1 - 0.99

α = 0.01

`(\alpha)/(2)=(0.01)/(2)=0.005`

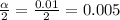
Solving further:

`\begin{gathered} 1-(\alpha)/(2) \\ \\ =1-0.005 \\ =0.995 \end{gathered}`

Using the z-table, we have:

P(Z < 2.575) = 0.995

Therefore, the critical value that corresponds to the confidence level of 99% is 2.575 which is approximately 2.58.

ANSWER:

2.58