The cosine rule is shown below:
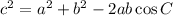
The small letters are the side lengths and capital letters are the angles.
From the triangle shown, we can write:
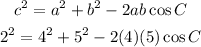
We can simplify and solve for the angle C. The steps are shown below:
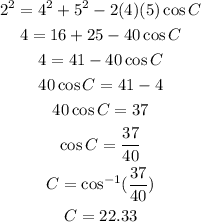
Now, we can find the value of "2ab cos(C)". Shown below:
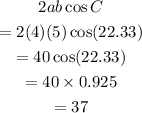
Thus, the answer is 37.
Correct Answer
A