To obtain the value of x, the following steps are necessary:
Step 1: Since both triangles CDE and FGE are similar, the following ratio is valid:
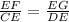
Step 2: Substitute the value of the lengths of the sides into the ratio as follows:
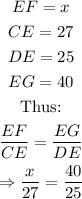
Step 3: Solve the resulting equation for x, as follows:
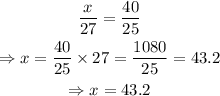
Therefore, the value of x is 43.2 (Option B)