Question

A quantity with an initial value of 890 grows continuously at a rate of 3-5% per decade. What is the value of the quantity after 99 years, to the nearest hundredth?

Answer 1

Let P represent the initial value

Let r represent annual growth rate

let n represent the number of periods

p = 890

r=3.5%

n = 10 ( since a decade is 10 years, 99 years after will be 10 decades)

the formula to calculate the value after 99 years is given by

`\begin{gathered} A=p(1+\text{ }(r)/(100))^n \\ \\ A=\text{ 890(1 + }(3.5)/(100))^(10) \\ A=890(1.035)^(10) \\ A=890(1.410598) \\ A=1255.432897 \\ A\cong1255.43\text{ ( nearest hundredth)} \end{gathered}`

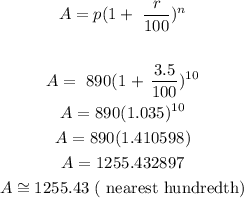
The value of the quantity after 99 years is 1255.43