Question

O GRAPHING=Finding the next terms of an arithmetic sequence with integersThe first three terms of an arithmetic sequence are as follows.+1, 2, 5Find the next two terms of this sequence.1, 2,5. 0 00 05x

Answer 1

`\begin{gathered} \text{fourth term}\rightarrow8 \\ \text{fifth term}\rightarrow11 \end{gathered}`

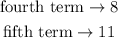
Step-by-step explanation

An arithmetic sequence is an ordered set of numbers that have a common difference between each consecutive term,it is give by the expression:

`a_n=a_1+(n-1)d`

so

Step 1

use the given data to find the arithmetic sequence

so

let

`\begin{gathered} a_1=-1 \\ a_2=2 \\ a_3=5 \end{gathered}`

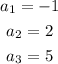
so

a) find the common difference

`\begin{gathered} \text{Difference}_1=a_2-a_1=2-(-1)=2+1=3 \\ \text{Difference}_1=5-2=3 \\ \end{gathered}`

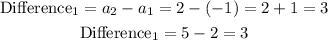
hence the common difference is 3

`d=\text{ 3}`

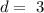
now, chec the first term and replace in the formula

`\begin{gathered} \text{first term}\rightarrow-1 \\ \text{difference}\rightarrow3 \\ \text{replace} \\ a_n=a_1+(n-1) \\ a_n=-1+(n-1)3 \end{gathered}`

Step 2

now, use the expression to find teh netx two terms

a)

`\begin{gathered} a_n=-1+(n-1)3 \\ \text{for n= 4,replace} \\ a_4=-1+(4-1)3 \\ a_4=-1+(3)3=-1+9=8 \\ a_4=8 \end{gathered}`

b) fifth term

`\begin{gathered} a_n=-1+(n-1)3 \\ \text{for n= 4,replace} \\ a_5=-1+(5-1)3 \\ a_5=-1+(4)3=-1+12=11 \\ a_5=11 \end{gathered}`

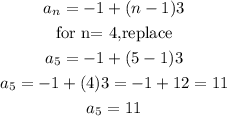
so, the answer is

`8,11`

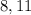
I hope this helps you