Question

Find the linear function with the following properties. f(-4) = -10 Slope of f = 4/3

Answer 1

The first condition gives us a point that belongs to the line.

The second condition gives us the slope of the line.

If we write the line equation as:

`f(x)=mx+b`

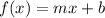
we have that m has a value of 4/3 (m=4/3) as it is defined by the second condition.

Then, we can calculate the other unknown, the y-intercept "b", using the other condition:

`\begin{gathered} f(-4)=((4)/(3))\cdot(-4)+b=-10 \\ (-16)/(3)+b=-10 \\ b=-10+(16)/(3)=(-30+16)/(3)=(-14)/(3) \end{gathered}`

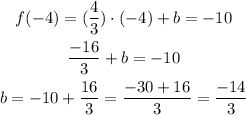
Then, with a slope of 4/3 and an y-intercept of (-14/3), the linear function can be written as:

`f(x)=(-4)/(3)x-(14)/(3)`