y = -21/2 x + 5 (option C)
Step-by-step explanation:
The points: (-4, 47) and (2, -16)
Using the slope formula:
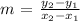
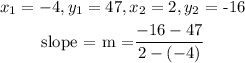
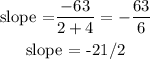
Equation of line in slope intercept form:
y = mx + b
b =y - intercept. To get b, we would use any of the given point and the slope
using (-4, 47) = (x, y)
47 = -21/2 (-4) + b
47 = 84/2 + b
47 = 42 + b
b = 47 - 42
b = 5
The equation in slope intercept form becomes:
y = -21/2 x + 5 (option C)