Given:
A large hose can fill a swimming pool In 45 hours.
A small hose can fill the same pool In 50 hours.
To find:
The required time to complete the task if both hoses are used together.
Step-by-step explanation:
One hour's work of large hose is,
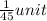
One hour's work of small hose is,
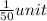
When both work together, the one hour's work
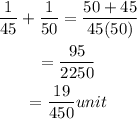
We know that time is inversely proportional to the work done.
Therefore,
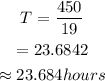
Thus, if both hoses are used to fill the pool, then the time required to complete the task is 23.684 hours.
Final answer:
The time required to complete the task when both hoses work together is 23.684 hours.