Question

stion 5 of 9A line in the coordinate plane passes through the point and is parallel to the line with equation .

Answer 1

The Solution:

We want to find the equation of a line S, which passes through point (6,2).

Let the required equation of line S be

`y-y_1=m(x-x_1)`

Where m = the slope of line S, and

`\begin{gathered} x_1=6 \\ y_1=2 \end{gathered}`

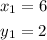
We are told that line S is parallel to line r, which is, y = 56x + 1. This implies that both lines have the same slope (m).

So, to find the slope (m) of line S, we shall compare y=56x+1 to the general form of equation of a line as given below:

`y=mx+c`

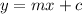
Comparing both equations below:

`\begin{gathered} y=mx+c \\ y=56x+1 \\ \text{ We have that,} \\ m=56 \end{gathered}`

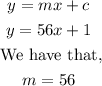
Substituting 56 for m, and the given point (6,2) in the formula above, we get

`y-2=56(x-6)`

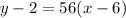
Clearing the bracket, we get

`\begin{gathered} y-2=56x-336 \\ y=56x-336+2 \\ y=56x-334 \end{gathered}`

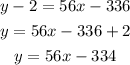
Thus, the equation of line r is: y = 56x - 334