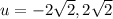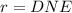Given:
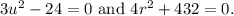
Aim:
We need to find the values of u and r.
Step-by-step explanation:
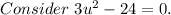
Divide both sides of the equation by 3.
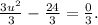

Add 8 to thte both sides of the equation.
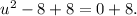
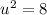
Take sqaure root on both sides.

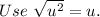
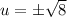
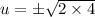
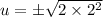
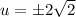
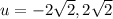
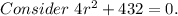
Divide both sides of the equation by 4.

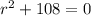
Subtract 108 from both sides of the equation.
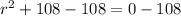
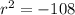
Take square root on both sides of the equation.
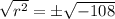
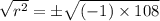
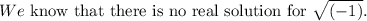
Final answer: