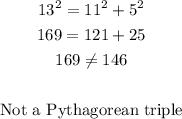Answer:
The correct option is option C
It is the only one that makes a right-angled triangle
Step-by-step explanation:
The dimensions that would make a right angle are the ones with the set of numbers that satisfies the Pythagorean theorem
The Pythagorean theorem state that in a right-angled triangle, the square of the hypotenuse is equal to the sum of squares of the opposite sides.
Knowing that the hypotenuse is always the longest side
Suppose x is the hypotenuse of a right angled triangle, and y and z are the opposite sides, then
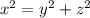
Let us check the given options one after the other to see which one is a Pythagorean Triple (satisfies the Pythagorean theorem).
A.
10, 8, 7
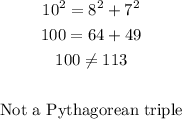
B.
31, 20, 21
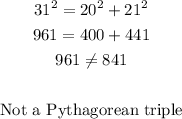
C.
9, 40, 41

D.
11, 13, 5