Question

OutcomeAnswer the following. Round your answers to the nearest thousandths.Number of SpinsExplanationCheckRed(a) From Donna's results, compute the experimental probability of landing on yellow.394аYellowJ420(b) Assuming that the spinner is fair, compute the theoretical probability of landing on yellow.(c) Assuming that the spinner is fair, choose the statement below that is true.O With a large number of spins, there might be a difference between the experimental andtheoretical probabilities, but the difference i need help with this math problem

Answer 1

ANSWERS

(a) 0.420

(b) 0.400

(c) With a large number of spins, there might be a difference between the experimental and theoretical probabilities, but the difference should be small

Step-by-step explanation

(a) The experimental probability is given by,

`P_(exp)=\frac{number\text{ }of\text{ }successes}{number\text{ }of\text{ }trials}`

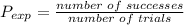
In this case, Donna spun the dial 1000 times and 420 times it landed on yellow,

`P_(exp)=(420)/(1000)=0.420`

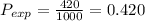
Hence, the experimental probability of landing on yellow is 0.420.

(b) The theoretical probability is given by the geometry of the spinner and, if it is fair, the number of yellow sections,

`P_(th)=\frac{number\text{ }of\text{ }favorable\text{ }outcomes}{total\text{ }posible\text{ }outcomes}`

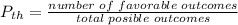
In this case, the spinner is divided into 10 equally sized slices, and 4 of them are yellow,

`P_(th)=(4)/(10)=0.400`

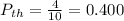
Hence, the theoretical probability of landing on yellow is 0.400.

(c) As we can see in parts a and b, for 1000 trials, the experimental and theoretical probabilities are almost the same - i.e. there is a small difference. This is known as the law of large numbers which states that if the number of trials of an experiment is large, the experimental probability of each event should be close to the theoretical probability.

Hence, the true statement is the first one: with a large number of spins, there might be a difference between the experimental and theoretical probabilities, but the difference should be small.