We let x be the length of the shortest side of the triangle. If the second side of the triangular deck is 5 ft longer than the shortest side, this can be represented as x + 5. For the third side, it has a length of 5 ft shorter than twice the length of the shortest side. This can be represented as 2x - 5. Given that we have a total perimeter of 64 ft, the sum of the length of the sides must be equal to this. We have
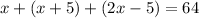
Solve for x, we get
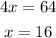
Hence, the length of the triangle are:
Shortest side = 16 ft
Second side = 16 ft + 5ft = 21 ft
Third side = 2(16ft) - 5 ft = 27 ft