Given the expression:
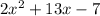
if we multiply it by 2/2, we get the following:
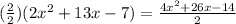
which we can write in the following way:
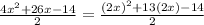
then, we can factor the numerator using 2x as a variable. Then, we have the following:
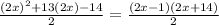
since the right factor has coefficients that are multiples of 2, we have:
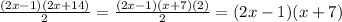
therefore, the final factorization is (2x-1)(x+7)