Question

Suppose that y varies directly as the square root of x, and that y = 48 when x = 144. What is y when x = 79? Round your answer to two decimal places if necessary

Answer 1

When two quantities (x , y) varies directly, means they increase together or decrease together, we use one of these rules

`\begin{gathered} y=kx \\ OR \\ (y_1)/(y_2)=(x_1)/(x_2) \end{gathered}`

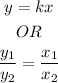
In the question, y varies directly with square root x, so the rule will be

`(y_1)/(y_2)=(√(x_1))/(√(x_2))`

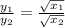
Since y is 48 when x = 144, then

`\begin{gathered} y_1=48 \\ x_1=144 \end{gathered}`

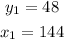
We need to find y when x = 79

`\begin{gathered} y_2=? \\ x_2=79 \end{gathered}`

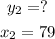
Let us substitute them in the rule

`(48)/(y_2)=(√(144))/(√(79))`

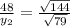
By using cross multiplication

`\begin{gathered} √(144)* y_2=48*√(79) \\ √(144)y_2=426.633332 \end{gathered}`

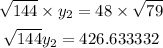
Divide both sides by square root 144

`\begin{gathered} (√(144)y_2)/(√(144))=(426.633332)/(√(144)) \\ y_2=35.552777 \end{gathered}`

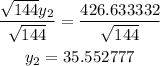
Round it to 2 decimal places

`y_2=35.55`

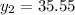
To check your answer look at the values of x and y

Since x decreased from 144 to 79, y also decreased from 48 to 35.55

So your answer is right

The value of y is 35.55