Answer:
z = 496.13
Step-by-step explanation:
Let the statement be written mathematically as follows:
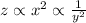
So that:
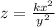
Where k is constant.
For z = 128, x = 8, and y = 9, we have:
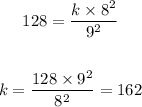
Using this value of k, we write the formula as:
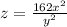
Now for x = 7, y = 4, we need to find z.
