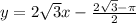Given:
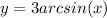
Let's find the equation of the tangent line over the interval:
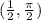
First find the derivative of the equation:
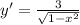
Now evaluate the derivative when x = 1/2:
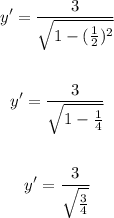
Solving further:
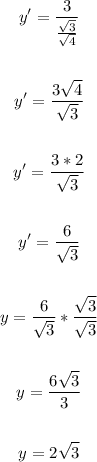
Now, the slope of the tangent line is 2√3.
Input the value for the slope, then put (1/2, π/2) for x1 and y1 in point-slope form:
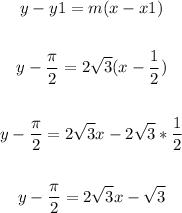
Now add π/2 to both sides:
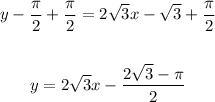
Therefore, the equation of the tangent line is:
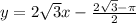
ANSWER: