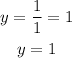Question

I need help with my pre-calculus homework, the image of the problem is attached below!

Answer 1

Holes: x = -2

y-intercept = (0, 3/4)

zero = (3, 0)

Vertical asymptote: x = 4

Horizontal asymptote: y = 1

Explanation:

We have the following function:

`f\mleft(x\mright)=(x^2-x-6)/(x^2-2x-8\:)=((x-3)\cdot(x+2))/((x-4)\cdot(x+2))=(x-3)/(x-4)`

Holes are avoidable discontinuities.

In this case, a discontinuity occurs when the denominator is 0, this happens when x = 4 or x = -2, but when x = -2, we can avoid it, therefore, x = -2 is a hole.

We calculate the y-intercept when x is equal to 0, therefore, we can calculate it like this:

`y=(0^2-0-6)/(0^2-2\cdot0-8\: )=(-6)/(-8)=(3)/(4)\rightarrow(0,(3)/(4))`

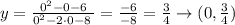
The zeros are the intercepts with x, and we calculate them when y is equal to 0, we calculate it like this:

`\begin{gathered} 0=(x-3)/(x-4) \\ x-3=0 \\ x=3\rightarrow(3,0) \end{gathered}`

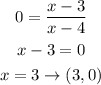
The vertical asymptote occurs in this case when the denominator is 0 and it is unavoidable, therefore:

`\begin{gathered} f(x)=(x-3)/(x-4) \\ x-4=0 \\ x=4 \end{gathered}`

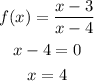
The horizontal asymptote is calculated as follows:

If the degree of the denominator is greater than the degree of the numerator, the horizontal asymmetry is the x-axis, y = 0.

If the degree of the numerator is 1 plus the degree of the denominator, the asymptote is a slanted asymptote of the form y = mx + b.

If the degrees are equal, the asintontate is the quotient of the principal coefficients of the numerator and denominator.

If the degree of the numerator is less than plus the degree of the denominator, there is no horizontal asymptote.

In this case, the degrees are equal, therefore:

`\begin{gathered} y=(1)/(1)=1 \\ y=1 \end{gathered}`