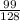Question

Find the probability of getting between 3 and 6 heads inclusive in 10 tosses of a coin

Answer 1

In the toss of a coin, the possible outcome is either head (H) or tail (T).

`\begin{gathered} \text{Number of heads (H) = 1} \\ \text{Number of tails (T) = 1} \\ \text{Total outcome = 2} \end{gathered}`
`\begin{gathered} \text{Probability}=\frac{\text{number of required outcome}}{\text{total possible outcome}} \\ \\ \text{Probability of head, P(H) =}(1)/(2) \\ \text{Probability of tail, P(T) =}(1)/(2) \\ \end{gathered}`

To get between 3 and 6 heads, inclusive, the following outcomes holds;

`\begin{gathered} 3\text{ heads, 7 tails = 3H, 7T}=\text{HHHTTTTTTT} \\ 4\text{ heads, 6 tails = 4H, 6T}=\text{HHHHTTTTTT} \\ 5\text{ heads, 5 tails = 5H, 5T}=\text{HHHHHTTTTT} \\ 6\text{ heads, 4 tails = 6H, 4T}=\text{HHHHHHTTTT} \end{gathered}`

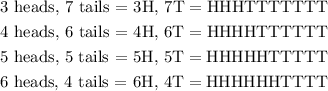
Probability of 3H, 7T using binomial distribution for the arrangement of the outcomes

`\begin{gathered} P(\text{HHHTTTTTTT)}=^(10)C_3((1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)) \\ P(\text{HHHTTTTTTT)=120}*((1)/(2))^(10) \\ P(\text{HHHTTTTTTT)}=120*(1)/(1024) \\ P(\text{HHHTTTTTTT)}=(120)/(1024) \end{gathered}`

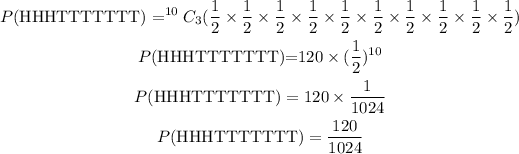
Probability of 4H, 6T using binomial distribution for the arrangement of the outcomes

`\begin{gathered} P(\text{HHHHTTTTTT)}=^(10)C_4((1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)) \\ P(\text{HHHHTTTTTT)=210}*((1)/(2))^(10) \\ P(\text{HHHHTTTTTT)}=210*(1)/(1024) \\ P(\text{HHHHTTTTTT)}=(210)/(1024) \end{gathered}`

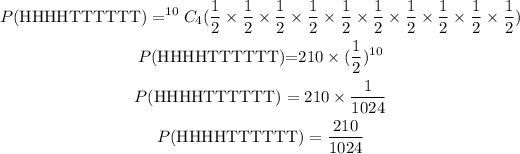
Probability of 5H, 5T using binomial distribution for the arrangement of the outcomes

`\begin{gathered} P(\text{HHHHHTTTTT)}=^(10)C_5((1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)) \\ P(\text{HHHHHTTTTT)=252}*((1)/(2))^(10) \\ P(\text{HHHHHTTTTT)}=252*(1)/(1024) \\ P(\text{HHHHHTTTTT)}=(252)/(1024) \end{gathered}`

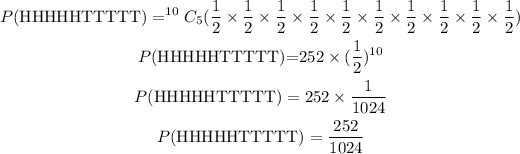
Probability of 6H, 4T using binomial distribution for the arrangement of the outcomes

`\begin{gathered} P(\text{HHHHHTTTTT)}=^(10)C_6((1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)*(1)/(2)) \\ P(\text{HHHHHTTTTT)=210}*((1)/(2))^(10) \\ P(\text{HHHHHTTTTT)}=210*(1)/(1024) \\ P(\text{HHHHHTTTTT)}=(210)/(1024) \end{gathered}`

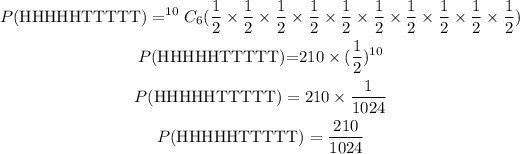
The probability of getting between 3 and 6 heads inclusive in 10 tosses of a coin will be the sum of the probabilities gotten.

`\begin{gathered} P(3\text{ and 6 heads inclusive)=}(120)/(1024)+(210)/(1024)+(252)/(1024)+(210)/(1024) \\ =(792)/(1024) \\ =(99)/(128) \end{gathered}`

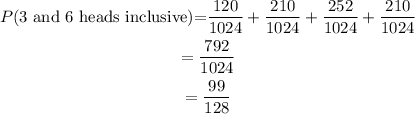
The probability of getting between 3 and 6 heads inclusive in 10 tosses of a coin is

`(99)/(128)`