Question

I need help with this question #4 it is timed

Answer 1

The probability (P) an Event A or an Event B occurs is P(A) + P(B).

The probability of an event A occuring is:

`P(A)=\frac{\text{ number of favorable outcomes of A}}{\text{ total number of outcomes}}`

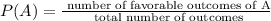
When rolling two dices, the sum can be:

If the result of the first dice is 1:

2, 3, 4, 5, 6, 7

If the result of the first dice is 2:

3, 4, 5, 6, 7, 8

If the result of the first dice is 3:

4, 5, 6, 7, 8, 9

If the result of the first dice is 4:

5, 6, 7, 8, 9, 10

If the result of the first dice is 5:

6, 7, 8, 9, 10, 11

If the result of the first dice is 6:

7, 8, 9, 10, 11, 12

Thus, there are 36 possible combinations.

From these combinations,

15 sums are less than 7

3 sums are greater than 10

Then, the probability of event A (sum is less than 7) is:

`P(A)=(15)/(36)=(5)/(12)`

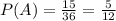
And the probability that event B (sum is greater than 10) occurs:

`P(B)=(3)/(36)=(1)/(12)`

Finally:

`\begin{gathered} P(A+B)=(15)/(36)+(3)/(36)=(18)/(36) \\ P(A+B)=(1)/(2) \end{gathered}`

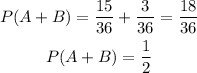
Answer: 1/2.