Question

As one part of a Mountain- Man triathlon, participants must row a canoe 5 mi down river (with the current), circle a buoy, and row 5 mi back up river (against the current) to the starting point. If the current is flowing at a steady rate of 4 mph, and Tom Chaney made the round-trip in 3 hr; how fast can he row in still water. ( hint: the time rowing down river and the time rowing up must add up to 3hr)

Answer 1

Tom Chaney can row 6 mph in still water.

Step-by-step explanation

Let the speed of Tom Chaney in still water be x.

Let the time taken to row downstream (with the current) be a.

Let the time taken to row upstream (against the current) be b.

We know that the speed of the river is 4 mph.

According to the rules of relative velocity, the real velocity of the boat with the current will be given as

Speed downstream = (Speed in still water) + (Speed of the river) = (x + 4) mph

The real speed of boat, rowing upstream, against the curent will be given as

Speed upstream = (Speed in still water) - (Speed of the river) = (x - 4) mph

Recall that speed itself is given as

Speed = (Distance)/(Time taken)

So, we can write an expression for rowing downstream and upstream for the boat.

Downstream

Speed = (x + 4) mph

Distance = 5 miles

Time = a hours

(x + 4) = (5/a)

x = (5/a) - 4 ...... equation 1

Upstream

Speed = (x - 4) mph

Distance = 5 miles

Time = b hours

(x - 4) = (5/b)

x = (5/b) + 4 ....... equation 2

We can equate these two values of x to obtain one equation

(5/a) - 4 = (5/b) + 4

(5/a) - (5/b) = 4 + 4

(5/a) - (5/b) = 8 ......... equation (*)

In the question, we are told to not that the total time add up to 3 hours. So,

a + b = 3 .......... equation (**)

Writing these two equations together

(5/a) - (5/b) = 8 ......... equation (*)

a + b = 3 .......... equation (**)

Making b the subject of formula in equation (**) and substituting this into equation (*)

a + b = 3

b = 3 - a

`\begin{gathered} (5)/(a)-(5)/(b)=8 \\ b\text{ = 3-a} \\ (5)/(a)-(5)/(3-a)=8 \\ \text{Multiply through by a(3-a)} \\ (5a(3-a))/(a)-(5a(3-a))/((3-a))=8a(3-a) \\ 5(3-a)-5a=8a(3-a) \\ 15-5a-5a=24a-8a^2 \\ 15-10a=24a-8a^2 \\ 8a^2-24a-10a+15=0 \\ 8a^2-34a+15=0 \end{gathered}`

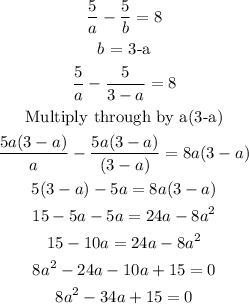
We then have to solve this quadratic equation, on solving, we obtain

8a² - 4a - 30a + 15 = 0

4a (2a - 1) - 15 (2a - 1) = 0

(4a - 15) (2a - 1) = 0

4a - 15 = 0 OR 2a - 1 = 0

4a = 15 OR 2a = 1

a = (15/4) OR a = (1/2)

a = 3.75 hours OR a = 0.5 hour.

But since we know that a and b add up to be 3 hours, so, the only feasible answer is a = 0.5 hour.

Recall b = 3 - a

b = 3 - 0.5 = 2.50 hours

We can now solve for the speed of the beat in still water this way

Recall that

x = (5/a) - 4

OR

x = (5/b) + 4

a = 0.5 hour, b = 2.5 hours

x = (5/0.5) - 4

x = 10 - 4 = 6 mph

OR

x = (5/b) + 4

x = (5/2.5) + 4

x = 2 + 4 = 6 mph

Hope this Helps!!!