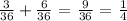The probability that the sum of the numbers rolled is either 7 or 10 is';
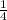
Here, we want to check if the sum of the numbers rolled is either 7 or 10
To do this, we need the right sample space
The sample space is as follows;
As we can see, the total number of expected results is 36
Now, we need the count of sums which are 7 or 10
The count of sums which are 7 is 6
The count of sums which are 10 is 3
The term 'or' between the probabilities mean that we are to add these fractions
We have this as;