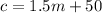Question

(m) Total Cost (c) 100 $200 200 $350 300 $500 500 $800 a function that models the total cost, c, to rent a large truck for any number of miles, m.

Answer 1

Given the table below:

To determine the function that models the total cost c, to rent a truck for any number of miles m, we use the line equation passing through two points.

The equation of a line that passes through two points is expressed as

`\begin{gathered} y-y_1=((y_2-y_1)/(x_2-x_1))(x-x_1)\text{ ---- equation 1} \\ where \\ (x_1,y_1)\text{ and \lparen x}_2,y_2)\text{ are the points through which the line passes.} \end{gathered}`

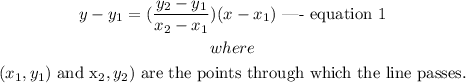
In this case,

`\begin{gathered} y\Rightarrow c \\ x\Rightarrow m \\ this\text{ gives} \\ c-c_1=((c_2-c_1)/(m_2-m_1))(m-m_1)\text{ ------ equation 2} \end{gathered}`

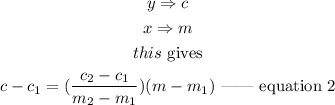
From the table of values,

`\begin{gathered} c_1=200 \\ m_1=100 \\ c_2=350 \\ m_2=200 \end{gathered}`

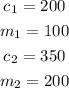
Substituting these values into equation 2, we have

`\begin{gathered} c-200=((350-200)/(200-100))(m-100) \\ \Rightarrow c-200=(150)/(100)(m-100) \\ \end{gathered}`

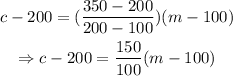
Multiply through by 100,

`\begin{gathered} 100(c-200)=100((150)/(100)(m-100)) \\ \Rightarrow100(c-200)=150(m-100) \end{gathered}`

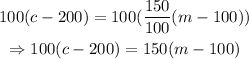
Open parentheses,

`100c-20000=150m-15000`

Add 20000 to both sides of the equation,

`\begin{gathered} 100c-20000+20000=150m-15000+20000 \\ \Rightarrow100c=150m+5000 \end{gathered}`

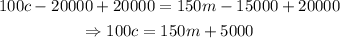
Divide both sides by the coefficient of c.

The coefficient of c is 100.

Thus,

`\begin{gathered} (100c)/(100)=(150m+5000)/(100) \\ c=(150)/(100)m+(5000)/(100) \\ \Rightarrow c=1.5m+50 \end{gathered}`

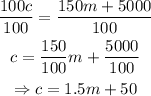
Hence, the function that models the total cost, c, to rent a large truck for any number of miles m is expressed as

`c=1.5m+50`