Question

Find the perimeter of the following shape, rounded to the nearest tenth:Options -12.46.919.122.8

Answer 1

Given:

The coordinates are,

`\begin{gathered} A(-3,5) \\ B(2,6) \\ C(0,2) \\ D(-5,1) \end{gathered}`

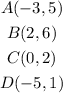
To find:

The perimeter

Step-by-step explanation:

We know that,

The perimeter is the sum of all sides.

So, let us find the distance between the adjacent coordinates.

The distance formula is,

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

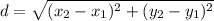
The distance AB is,

`\begin{gathered} AB=√((2+3)^2+(6-5)^2) \\ =√(5^2+1^2) \\ =\sqrt{26\text{ }}units \end{gathered}`

The distance BC is,

`\begin{gathered} BC=√((0-2)^2+(2-6)^2) \\ =√(2^2+4^2) \\ =\sqrt{20\text{ }}units \end{gathered}`

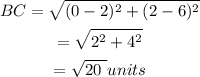
The distance CD is,

`\begin{gathered} CD=√((-5-0)^2+(1-2)^2) \\ =√(5^2+1^2) \\ =\sqrt{26\text{ }}units \end{gathered}`

The distance DA is,

`\begin{gathered} DA=√((-3+5)^2+(5-1)^2) \\ =√(2^2+4^2) \\ =\sqrt{20\text{ }}units \end{gathered}`

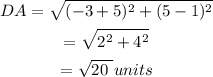
Therefore, the perimeter is

`\begin{gathered} P=AB+BC+CD+DA \\ =√(26)+√(20)+√(26)+√(20) \\ =2√(26)+2√(20) \\ P=19.14 \\ P\approx19.1units \end{gathered}`

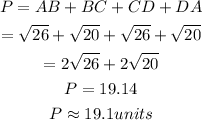
Thus, the perimeter of the given shape is 19.1 units.

Final answer:

The perimeter of the given shape is 19.1 units.