Question

Function gis represented by the equation.g(x)=-20(1/2)^x+10Which statement correctly compares the two functions on the interval [-2, 1]?

Answer 1

First we find the values for the function g in the interval [-2,1].

x = -2

`g(-2)=-20((1)/(2))^(-2)+10=-70`

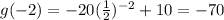
x = -1

`g(-1)=-20((1)/(2))^(-1)+10=-30`

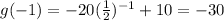
x = 0

`g(0)=-20((1)/(2))^0+10=-10`

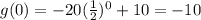
x = 1

`g(1)=-20((1)/(2))^1+10=0`

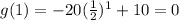
Statement

Function f is increasing.

Function g is increasing.

Function f is negative.

Function g is negative.

Answer: D. Both functions are increasing, but function g increases at a faster average rate.