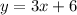First, we check that the three points are collinear.
Given three points (x1,y1), (x2,y2), and (x3,y3), then the three points are collinear if the following condition is satisfied.
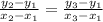
In our case, we can set
(x1,y1) =(-2,0), (x2,y2) = ( 4, 18)and (x3,y3) = (5, 21)
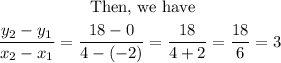
And

Hence
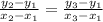
Therefore, the points (-2,0), ( 4, 18), and (5, 21) are collinear.
Given two points (x1,y1) and (x2,y2) on the Cartesian plane, then the gradient, m, of the line that passes through them is given by

Then, the gradient of the line passing through (-2,0), ( 4, 18) is 3
Given a point (x1,y1) on the Cartesian plane, and a line that passes through the point with gradient, m, then the equation of the line is given by

Therefore,

That is the equation is