Answer:
z=-10.57
Step-by-step explanation:
The test statistic for a population proportion is given by:
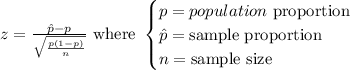
In the given problem, the parameters are:
• n=1015
,
• p(hat)=83%=0.83
,
• p=92%=0.92
Substitute into the formula above:
![\begin{gathered} z=\frac{0.83-0.92}{\sqrt[]{(0.92(1-0.92))/(1015)}}=\frac{-0.09}{\sqrt[]{(0.92*0.08)/(1015)}} \\ z=-10.57 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m39eeewvxxz9xz8p2w2h4c8cyjpu9o1yui.png)
The value of the test statistic is -10.57 (correct to 2 decimal places).