We are given a 45°-45°-90° triangle which is a special type of an isosceles triangle.
Isosceles triangle means a triangle in which two sides are equal.
The length of the hypotenuse is 24 inches.
The ratio of the lengths between the hypotenuse and one of the sides is given by
![\begin{gathered} x=\sqrt[]{2}\cdot h \\ x=\sqrt[]{2}\cdot24 \\ x=24\sqrt[]{2}\; \; \text{inches} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vq33stozc4w91cwm4wwmkpfjuwxdl7q9a1.png)
This means that the length of the other two sides is 24√2 inches each.
Recall that the area of a triangle is given by
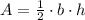
Where b is the base and h is the height of the triangle.
So, we have
b = 24√2 inches
h = 24√2 inches
So, the area becomes
![\begin{gathered} A=(1)/(2)\cdot b\cdot h \\ A=(1)/(2)\cdot24\sqrt[]{2}\cdot24\sqrt[]{2} \\ A=(1)/(2)\cdot1152 \\ A=576\; \; in^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/s9bor73lcxd51n35v7daswdz785p9jjic5.png)
Therefore, the area of the given 45°-45°-90° triangle is 576 square inches.