Given that:
- Francesca spent $30 on 6 boxes of pencils and 9 boxes of ballpoint pens.
- Terrence spent $18 on 7 boxes of pencils and 2 boxes of ballpoint pens.
Let be "p" the cost (in dollars) of a box of pencils and "b" the cost (in dollars) of a box of ballpoint pens.
You can write the following equation to represent the total cost (in dollars) of 6 boxes of pencils and 9 boxes:
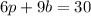
And you can write the second equation to represent the total cost (in dollars) of 7 boxes of pencils and 2 boxes of ballpoint pens:
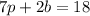
Having these equations, you can set up the following System of Equations to describe the situation given in the exercise:
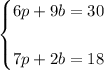
In order to solve it, you can use the Elimination Method:
1. Multiply the first equation by 7 and the second equation by -6:
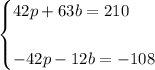
2. Add the equations:
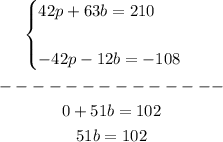
3. Solve for "b":
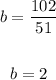
4. Substitute the value of "b" into one of the original equations:

5. Solve for "p":
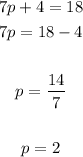
Hence, the answer is:
- Cost of a box of pencils: $2.00
- Cost of a box of ballpoint pens: $2.00