a) Good coins are supposed to come up heads 3/4 = 75% of the time.
Them, the probability of passing good coins is given by:
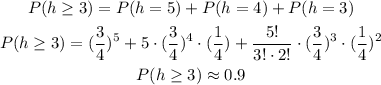
Then, the probability of discarding good coins is 1 - 0.9 = 0.1
b) Defective coins are supposed to come up heads 1/2 = 50% of the time.
Them, the probability of passing good coins is given by:
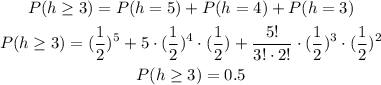
c) We know that 20% of the coins are defective.
To finde the fraction of coins that were discarded, we can aply the bayes theorem. Let P(G|D) be the probability of getting a good coin given it was discarded. Then we have:
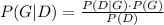
From part a, we know that P(D|G) = 0.1. And we also know that 80% of the coins are good, then P(G) = 0.8. Since 20% of the coins are defective, we have P(D) = P(G and D)+P(Defective and D) = 0.8*0.1 + 0.2*0.5 = 0.18
Them we have:
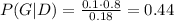
d) The cost is P(G)*P(D|G)*2 + P(Defective)*(1-P(D|Defective))*5 = 0.8*0.1*2 + 0.2*0.5*5 = $0.66